27: 2021/02/08(月) 17:30:35.45 0.net
>>1
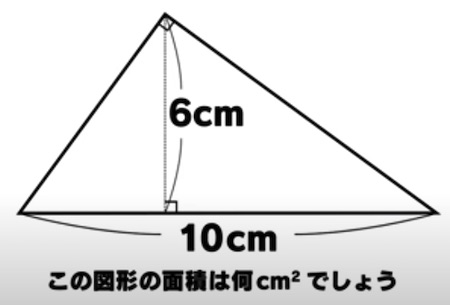
頂点を通る円を書くと半径は5cm
一番上の頂点から円の中心(10cmの辺の中点)を結んだ線分も5cmとなり
一番上の頂点から10cmの辺に下ろした垂線が5cmより長くなることはない
頂点を通る円を書くと半径は5cm
一番上の頂点から円の中心(10cmの辺の中点)を結んだ線分も5cmとなり
一番上の頂点から10cmの辺に下ろした垂線が5cmより長くなることはない
36: 2021/02/08(月) 17:34:08.10 0.net
>>1
上の角が直角とあるので
三角形の外接円を考えると直径10cmの高さは最大でも5cm
つまり高さ6cmが間違いか上の角が直角とあるのが間違い
上の角が直角とあるので
三角形の外接円を考えると直径10cmの高さは最大でも5cm
つまり高さ6cmが間違いか上の角が直角とあるのが間違い
198: 2021/02/09(火) 00:49:19.34 0.net
>>1
中学3年生で習う「円周角の定理」により「円周角が直角になる=対する辺は直径」となります
つまり直径が10cmですから半径は5cmとなります
直径10cmを底辺とする時に高さは半径(5cm)以下となりますから設問の高さ6cmは矛盾
したがって「以上の証明により設問のデータは矛盾している」が正答
義務教育の範囲内です
中学3年生で習う「円周角の定理」により「円周角が直角になる=対する辺は直径」となります
つまり直径が10cmですから半径は5cmとなります
直径10cmを底辺とする時に高さは半径(5cm)以下となりますから設問の高さ6cmは矛盾
したがって「以上の証明により設問のデータは矛盾している」が正答
義務教育の範囲内です
3: 2021/02/08(月) 17:18:11.10 0.net
どう間違えんの
4: 2021/02/08(月) 17:18:54.55 0.net
1%が間違えるんならわかるけど
5: 2021/02/08(月) 17:19:05.11 0.net
30じゃねえの?
6: 2021/02/08(月) 17:19:46.74 0.net
やっぱり分かってないなwww
7: 2021/02/08(月) 17:19:51.56 0.net
間違えようがないだろ
斜めの半分は最大でも5cmだから
6cmなんて実現不可能だし
斜めの半分は最大でも5cmだから
6cmなんて実現不可能だし
8: 2021/02/08(月) 17:20:23.32 0.net
こんな三角形は存在しない
9: 2021/02/08(月) 17:21:38.44 0.net
なんだろうなんかものすごい違和感ある
10: 2021/02/08(月) 17:21:51.68 0.net
なぞなぞかよw
11: 2021/02/08(月) 17:22:20.46 0.net
問題が間違ってんのかよ
12: 2021/02/08(月) 17:22:49.77 0.net
すまん、解説してくれ
13: 2021/02/08(月) 17:23:17.21 0.net
問題が間違いなら加点じゃねえの?
14: 2021/02/08(月) 17:24:13.52 0.net
三角形の面積じゃなくて
図形の面積って書いてあるのが何か関係ある?
図形の面積って書いてあるのが何か関係ある?
15: 2021/02/08(月) 17:25:12.61 0.net
高さが6cmはありえないが正解っぽい
17: 2021/02/08(月) 17:26:16.03 0.net
理由が分からない
18: 2021/02/08(月) 17:26:51.86 0.net
60!
19: 2021/02/08(月) 17:27:10.32 0.net
問題のミスプリで正解率100%だな
22: 2021/02/08(月) 17:27:40.91 0.net
図形がどうであれ三角形でたて6cmよこ10cmと書いてあるなら30cm2の答え以外ないだろ
23: 2021/02/08(月) 17:28:26.18 0.net
>>16
なんで5cmなのかが分からない
なんで5cmなのかが分からない
24: 2021/02/08(月) 17:29:18.26 0.net
10cmを直径とする円を書いてみれば6cmがおかしいのがすぐ分かる
[ad_fluct2]
26: 2021/02/08(月) 17:29:59.51 0.net
底辺(10)X高さ(6)÷2=30でしよ?
28: 2021/02/08(月) 17:30:42.69 0.net
定規を使え
33: 2021/02/08(月) 17:33:18.49 0.net
直角を頂点とする軌跡は底辺を直径とする弧になるから
高さは最大で半径分の5cmになるわけか
高さは最大で半径分の5cmになるわけか
34: 2021/02/08(月) 17:33:19.81 0.net
図形の形状が正しいとすれば高さは4.8cmくらいか
37: 2021/02/08(月) 17:34:10.78 0.net
You Tubeにあったよこれ


25cm2
出題側が底辺10で高さ6にしてるんだから、変な理屈捏ねずに数秒で30cm2って書いてさっさと次の問題に進むのが正解
これに時間かけたところでどうせ全員加点になる。ドヤ顔で時間かける奴は負け組
※2 だからお前は底辺の大人になったんだよ
昔:グダグダ理屈ごねてねぇで、言われた通りやってろ!
今:なるほどな。有能!
問題に不備がないとすれば、10cmって書いてるところが直線とは限らんだろ。
2つの辺の合計が10cmってだけ。
面積を求めるだけならわざわざ書く必要のない上の頂点の角度があえて書いてあるのがポイント。
つまり問題が間違っているのではなく「存在しない」が出題者意図する解答。
※6
球面3角形ならあそこが90度でも成り立つぞ。
存在しないとするのは早合点
球面3角形ならそれ書かなきゃ面積なんて求められんじゃん、「この図形が存在する場合の面積は何㎝2でしょう」ならともかくさ、そもそも1部が成り立っても長さも適合させた球体ある?